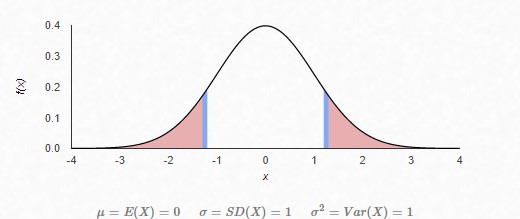
Anomaly Detection is a widely used for Machine Learning as a service to find out the abnormalities in a system. The idea is to create a model under a probabilistic distribution. In our case, we will be dealing with the Normal (Gaussian) distribution. So, when a system works normally it’s features reside under a normal curve. And when it behaves abnormally, it’s features move to the far ends of the normal distribution curve. Middle area shows distribution of normal behavior and the red areas on the far ends show distribution of abnormal behavior. If you already don’t know, you should read the concepts of Mean, Variance and Standard Deviation first. In the next paragraphs I’ll be addressing how do we create a distribution curve for our system? The system I work on generates a file, daily. Having different number of lines in it every day. There is no defined range for the number of lines it should have. So, my problem was how to auto-detect if the file for today had too low number of lines or too high number of lines.
Now that I had data for two weeks. I could find out the mean (average) number of lines. On the distribution curve in Figure 1, this would be the middle of the curve horizontally, i-e 0 on the x axis. But in the list of line counts above, it can be seen that actual values deviate from the mean, which is 55728.722222 in this case. For example, take 68336 which is reasonably away from the mean. I had the valid data, but I no false examples. That is, the examples that will guage the accuracy of my anomaly detection system. What I did was added a few examples that I consider as anomalous, and see if my system learns and predicts correctly.
It could be seen that our original data follows a pattern. Whereas the false examples we added later are scattered away. Those are the outliers we want to catch!! Let’s do some calculations to get mean and variance of our training dataset. What we do here is use mean and variance to model a normal (Gaussian) distribution like the one shown in Figure 1. And then we calculate f1score to find out a value (Epsilon) which we can set as best decisive threshold between our normal and abnormal values. [sharethis-inline-buttons]